

The systems project for CS265 is designed to provide background on state-of-the-art systems, data structures, and algorithms. It includes a design component and an implementation component in C or C++, dealing with low level systems issues such as memory management, hardware conscious processing, parallel processing, managing read/write tradeoffs, and scalability. Systems projects will be done individually, each student is required to work on their own. This is a focused project that should not necessarily result in many lines of code (like the cs165 project), but will exercise your understanding of modern system design issues and tradeoffs.
The goal of the project is to build a modern write-optimized NoSQL key-value store. The system will be based on a state-of-the-art variant of LSM-tree (Log Structured Merge tree) design. There are two parts in the project. In the first part, you will build a basic single thread key-value store that will include all major design components as in state-of-the-art key-value stores. In the second part, you will extend the design to support multiple threads and be able to process multiple queries in parallel, while utilizing all cores of a modern server machine.
Students that finish the systems project quickly and want to work on research will be able to do so by exploring open research topics directly on top of their LSM-tree. We have plenty of open topics in this area.
As storage becomes cheaper, and modern applications require both efficient lookups and updates, LSM-trees provide a good balance between the two by avoiding expensive in-place updates. They work by buffering writes (inserts, deletes, and updates) in main memory and deferring their persistence to a later time. While such designs slightly penalize reads, which then need to search various different levels of data structures, they allow writes to be performed efficiently, and dramatically increase data ingestion rates.
Today, LSM-trees are used in a variety of systems, typically key-value stores, as a means of fast indexing of heavily updated data. Google’s LevelDB and BigTable, Facebook's RocksDB, Apache's Cassandra, and numerous research prototypes use LSM-trees or similar variants as the core data structure for storage.
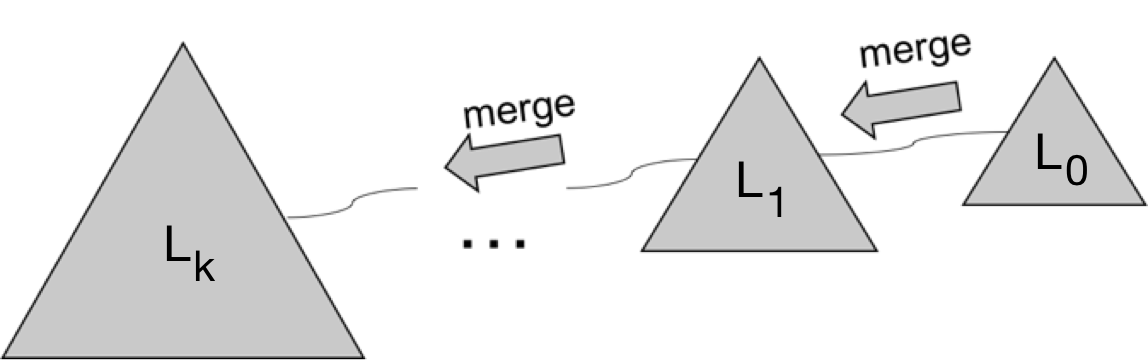

Data Layout. An LSM-tree consists of a hierarchy of storage levels that increase in size. The first level, called the buffer (and L0 in some implementations), is generally the smallest and stored in main memory, and its purpose is to buffer updates for efficiency. Often, designs assign a separate data structure to the buffer, intended just for in-memory performance (e.g. skiplist, heap, etc). The rest of the levels are stored on disk. As new writes accumulate and the buffer fills, the buffer contents must be persisted to disk as a file with contents sorted on key order. The concept of a level is logical. A single level has two defining basic attributes which guide how the LSM Tree grows in size. The first is a capacity or threshold size (which may be expressed in bytes, or multiples of the buffer size), the second is a merge threshold for maximum number of runs allowed at that level; the merge threshold defines the merge policy for a level - leveling (one run allowed) or tiering (more than one run allowed). A run is a collection of one or more sorted files with non-overlapping key ranges. Files reside on the file system, and each file internally contains entries sorted on key order. Files are immutable, abide by an implementation specific format (e.g. SSTable for RocksDB); besides holding the data entries they can also persist smaller indexes (e.g. fences) or filters (e.g. Bloom) to help guide search within a file (this is explained more in the Lookups section). The figure above gives a high level visual of an LSM-tree.
Writes. Writes in LSM-trees are fast since they are always first performed in main memory (the buffer) and they are batch moved to the disk at later phases. Updates and inserts are treated in the same way, since they both bind a new specified value to a particular unique key in the key-value store. Deletes are also performed in the same way as updates (first added to buffer), but with a special marker, which denotes this record as "deleted". Since each level of an LSM-tree is restricted in size using thresholds, each of these operations are merged to the largest levels of the LSM-tree in a deferred and batched method. This process is called merging (or compaction) and is triggered when a level reaches its threshold size (capacity). For instance, a merge would be required when the buffer fills.
Merging (Compaction). The merge process takes as input a set of sorted files and creates as output a new set of sorted files non-overlapping in key range, called a run. Merges may be necessary in two conditions. In the first condition, the current level has reached its threshold size, therefore its contents needs to be pushed to larger levels as part of the merge process to clear more space at the current level. In the second condition, a new run is being moved into the current level which has already reached its allowed threshold of runs, and therefore any run being merged into the current level cannot simply be added, rather it must be merged with a run that is already at the current level in order to abide under the threshold. In this fashion, it is possible for a merge to cause a cascade of further merges through the larger levels that follow. Different implementations of merge may use different strategies for selecting contents (what and how much) to push into the next level. In this basic description, the merge pushes one run at a time between levels (select the entire contents of the current level as a run to push to the next level). For instance, initially a run is constructed on the data of L0 and flushed to the next level. If the flushed run now also causes L1 to reach its capacity threshold, then this run is sort merged with the contents of L1, forming one larger run and pushed one level larger in a cascading way. When data are sort-merged, deletes and updates are performed, keeping only the newest values when there are entries that modify the same key. This process can be seen in the figure above on the right hand side. Existing literautre contains several implementations of compactions such as, Optimizing Space Amplification in RocksDB and external sorting.
Lookups. A single key lookup is performed first in L0, and if no match is found, this lookup is propagated to larger levels of the tree from the most recent (smallest) to the oldest (largest). Range queries are also evaluated against all levels of the tree. To avoid doing a binary search on every single run during query answering, various optimizations can be performed by maintaining auxiliary structures. Common ones are: fence pointers and Bloom filters. Fence pointers are ranges formed by the minimum and/or maximum keys of each page (or every X pages), allowing a lookup to access only the part of a run with the range relevant to the target key. Stricly speaking, when we use leveling merge policy, for fence pointers we only need either the minimum or maximum, since all key ranges are sorted and non-overlapping within a level. Bloom filters on the other hand are used to speed up single key searches: if the bloom filter on a run returns false for a given target key, we don’t need to search that run for the target key. Some implementations elect to rebuild these optimizations in memory at every database startup, while other implementations keep these auxiliary structures persisted to disk and load them into memory as needed.
Consistency and Level Management. While files have correspondence with the underlying file system, levels are conceptual and must be managed by the LSM-tree implementation. To maintain a consistent view of the immutable files, it is typical to maintain globally a catalog and manifest structure (in-memory and persisted) which describes the file to level relationships and indicate which set of files form a current snapshot. That way, background merges that create new files can continue progress while ongoing readers are guaranteed to see a consistent view of the set of files corresponding to a single snapshot of the LSM-tree without disruption to query correctness.
The project is divided into two parts. The first part is about designing the basic structure of an LSM-tree for reads and writes, while the second part is about designing and implementing the same functionality in a parallel way so we can support multiple concurrent reads and writes. Each part will have a first milestone: a design document. Here you will discuss your design and development strategy and get feedback from the teaching staff. If you are stuck with how to proceed with a design document, check out the template here.
The project is purposely left open ended. You have complete freedom in how you design each part of your key-value store to achieve as much functionality as possible. For example, each level of the LSM-tree may be designed in its own way; each level may be a complex data structure itself, like a tree, or a plain one, like a simple array. The choice usually depends on the size of the available memory and the intended purpose of the design. We do expect a "minimum design".
Note: During compaction, as the number of levels increase, merging the content of the deeper levels of the tree will demand more memory. An alternative is to use external sorting in which data is brought into memory in chunks, sorted, and written to a temporary file. Then, the sorted files are merged and written back to disk. However, this process is still slow due to high I/O cost of moving the entire data (residing at the two levels) to memory and writing to disk. A commonly used approach is partial compaction in which one or more files of level-L are selected and merged with the overlapping files in level-(L+1), after which the merged files from level-L and level-(L+1) are removed. This reduces the overall data movement cost thereby being significantly faster and less memory-intensive.
Additionally, each student should describe, implement, and evaluate at least three different optimizations that support the performance requirements. The purpose of the optimizations is to approach improving your system design and performance from both a theoretical and empirical approach. These may include but not be restricted to altering the size ratio between the levels, the choice of the buffer data structure design, whether each level will consist of one or more structures (e.g., sorted arrays), how merging happens and when it is triggered, and many more design decisions that are open to the designer (you).
You can find us during OH to discuss your design and ideas for optimizations. Once you are done with the basic design, research opportunities begin as there are many open opportunities in the design space of LSM-trees.
Midway check-in (March 10)
Final Project Deliverable and Evaluations (After Reading Period)
There are three deliverables for the midway check-in:
Regarding the design document, we expect max 3 pages describing the basic design. That is we expect a description of the data layout in detail and a description of the dictionary operations. E.g., we would like to see the strategy you will follow to support put and get, etc. You should try to provide pseudocode, a graphic example, and the complexity analysis for both the operations.
The final deliverable consists of:
Evaluation Meeting
Each student with a systems project will have two 30 minute evaluation meetings
at the end of the semester. A code review and demo meeting with the TFs and an
experimental analysis meeting with Stratos. For remote students the evaluation
meeting will take place via Zoom and screen sharing.
Code Deliverable
The code deliverable of this project is an LSM-Tree implementation (both single threaded and parallel) with a number of tunable parameters: size ratio between levels, storage layer used for each level (RAM, SSD, HDD), different merging strategies, and any additional tuning parameters the students design. The final LSM-Tree is expected to support high update throughput (in the order of 100K-1M updates per second for flash storage and 1K-10K of updates per second for HDD storage), while at the same time provide efficient reads (in the order of 1K-5K reads per second for flash storage and 20-100 reads per second for HDD storage). For range queries, the performance of a short range query can ideally be close to point query performance whereas the performance of a long range query depends on selectivity. However, the performance should asymptotically be better than simply querying every key in the range using GET. The parallel LSM-Tree is expected to scale with number of cores, that is, we expect to see that as the number of cores used increases the performance of the tree is precipitously increasing. The software will be submitted as a code.harvard repository with at least read access for the teaching staff. code.harvard is Harvard's own enterprise version of Github.com. You can login to code.harvard here.
Final Report
The students are expected to generate a report presenting their final design, as well as the behavior and performance of their system. This report will be structured as a short systems research paper, having the following sections:
Live Demo
Students are expected to create a demonstration scenario where they will show the behavior of their LSM-Trees. In essence we expect to see in the demo different datasets and workloads that will lead to different behavior of the LSM-Tree in order to get a clear idea about its behavior. For example, a workload consisting of skewed updates (inserting values from a small set of values again and again) and a workload consisting of evenly distributed updates, will lead to different behavior of the system. Combining this, with either skewed or evenly distributed reads we get four workloads that will behave very differently. We expect to see such cases in the demo in order to understand the trade-offs of the LSM-Tree designed.
The demo is expected to have a 10/15-minute duration, focusing on the design decisions and the knobs used in the presented LSM design. A code review will also take place during this time. Students are expected to be able to quickly make changes in their code to adjust behavior and rerun experiments.
We provide a domain specific language along with tests and expected results. As well as a data/workload generator, which can be found here. The purpose of this is to allow you as much flexibility in your design and API as possible while still allowing for testing on our part. Every project will support six commands: put, get, range, delete, load, and print stats. Each command is explained in greater detail below.
The put command will insert a key-value pair into the LSM-Tree. Duplicates are not supported in the expected implementation so the repeated put of a key updates the value stored in the tree.
Syntax
p [INT1] [INT2]
The 'p' indicates that this is a put command with key INT1 and value INT2.
Example:
p 10 7
p 63 222
p 10 5
First the key 10 is added with value 7. Next, key 63 is added with value 222. The tree now holds two pairs. Finally, the key 10 is updated to have value 5. Note that the tree logically still holds only two pairs. These instructions include only puts therefore no output is expected.
The get command takes a single integer, the key, and returns the current value associated with that key.
Syntax
g [INT1]
The 'g' indicates that this is a get for key INT1. The current value should be printed on a single line if the key exists and a blank line printed if the key is not in the tree.
Example:
p 10 7
p 63 222
g 10
g 15
p 15 5
g 15
output:
7
5
Here we first put (key:value) 10:7, then 63:222. The next instruction is a get for key 10, so the system outputs 7, the current value of key 10. Next we try to get key 15 but it is not included in the tree yet so a blank line is generated in the output. Next we put 15:5. Finally, we get key 15 again. This time it outputs 5 as the key exists at this point in the instruction list.
The range command works in a similar way to get but looks for a sequence of keys rather than a single point.
Syntax
r [INT1] [INT2]
The 'r' indicates that this is a range request for all the keys from INT1 inclusive to INT2 exclusive. If the range is completely empty than the output should be a blank line, otherwise the output should be a space delineated list of all the found pairs (in the format key:value); order is irrelevant.
Example:
p 10 7
p 13 2
p 17 99
p 12 22
r 10 12
r 10 15
r 14 17
r 0 100
output:
10:7
10:7 12:22 13:2
10:7 12:22 13:2 17:99
In this example, we first put a number of keys and then collect the values with the range command. The first range prints only the pair 10:7. The pair associated with key 12 is not printed because ranges are half open: [lower_key, higher_key). The next range doesn't include key 17 but captures the others. The range [14,17) is empty so a blank line is output. Finally an oversized range captures all of the pair.
The delete command will remove a single key-value pair from the LSM-Tree.
Syntax
d [INT1]
The 'd' indicates that this is a delete command for key INT1 and its associated value (whatever that may be). A delete of a non-existing key has no effect.
Example:
p 10 7
p 12 5
g 10
d 10
g 10
g 12
output:
7
5
First the two pairs 10:7 and 12:5 are put into the tree. Next, we get key 10 which outputs the value 7. Key 10 is then deleted which generates no output. When we then try to get key 10 a second time we get a blank as the key has been deleted. Finally we get key 12 which is unaffected by the delete and therefore outputs the value 5.
The load command is included as a way to insert many values into the tree without the need to read and parse individual ascii lines.
Syntax
l "/path/to/file_name"
The 'l' command code is used for load. This command takes a single string argument. The string is a relative or absolute path to a binary file of integers that should be loaded into the tree. Note that there is no guarantee that the new values being inserted are absent from the current tree or unrepeated in the file, only that all of the pairs are puts in the order of the file.
Example:
l "~/load_file.bin"
This command will load the key value pairs contained in load_file.bin in the home directory of the user running the workload. The layout of the binary file is
KEYvalueKEYvalueKEYvalue...There is nothing but key-value pairs in the file. The first 4 bytes are the first key, the next 4 bytes are the first value and so on. Thus, a file of 32768 bytes has 4096 key value pairs to be loaded (though there could be fewer than 4096 pairs once loaded due to existing keys in the tree or duplicated keys in the file).
The print stats command is a command that allows the caller to view some information about the current state of the tree. This is helpful for debugging as well as the final evaluation. Each implementation may vary somewhat but at a minimum the function must include: (1) the number of logical key value pairs in the tree Logical Pairs: [some count]; (2) the number of keys in each level of the tree LVL1: [Some count], ... , LVLN [some count]; (3) a dump of the tree that includes the key, value, and which level it is on [Key]:[Value]:[Level].
Syntax
s
The 's' command code is used for printing stats. This command takes no arguments and prints out the stats for the tree.
Example:
This command will print out at a minimum the data listed above. For a very small tree one output might look like:
Logical Pairs: 12
LVL1: 3, LVL3: 11
45:56:L1 56:84:L1 91:45:L1
7:32:L3 19:73:L3 32:91:L3 45:64:L3 58:3:L3 61:10:L3 66:4:L3 85:15:L3 91:71:L3 95:87:L3 97:76:L3